SRM 735 MaxSquare 「よくある二分探索の変なことをやるやつ」

なんやこのテク...っていう気持ちになったので記事を書きます

http://community.topcoder.com/stat?c=problem_statement&pm=14929

問題の解説...https://www.topcoder.com/blog/single-round-match-735-editorials/

りんごさんの参考解説動画(ICPCの類似した問題)

https://youtu.be/agCN6bPxeE4?t=6052

https://youtu.be/agCN6bPxeE4?t=11979

問題の本質

数列Bが与えられる.
このときf(i,j) = (B[j] - B[i]) * (j - i + 1)の最大値を求めよ.

平面で考えてみる

横軸をindex,縦軸をBの値のと置くと、下のような図ができて

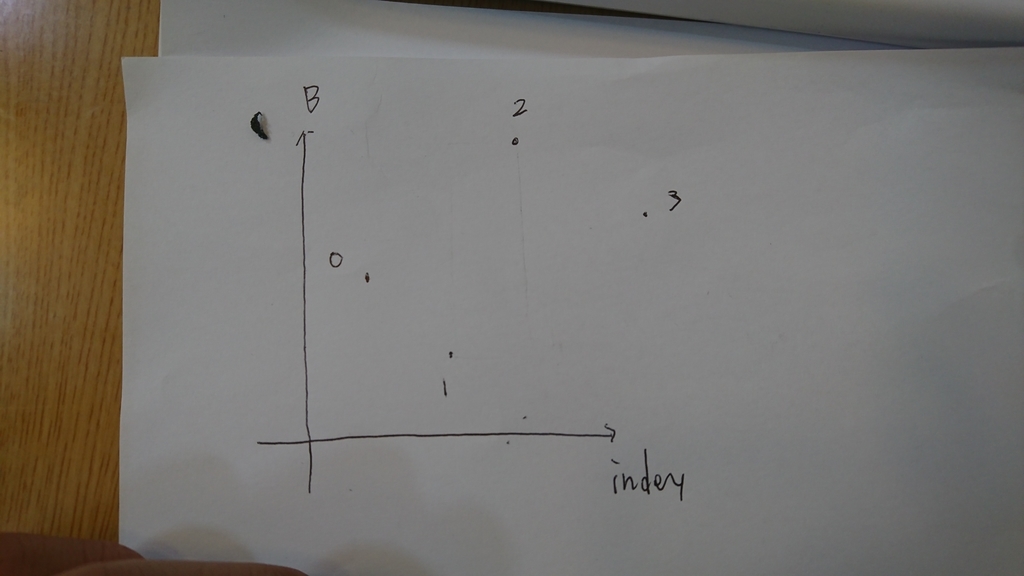
この図でf(1,2)は、下の長方形の面積になります.'

これの最大を求めたい...

最適な右上

ある頂点iを決めたとき、f(i,j)が最大になるjを「最適な右上」と呼ぶことにします.

左下になり得る頂点、右上になり得る頂点

こんな感じになりそう(実際なって証明ができるがなんとなくわかる)

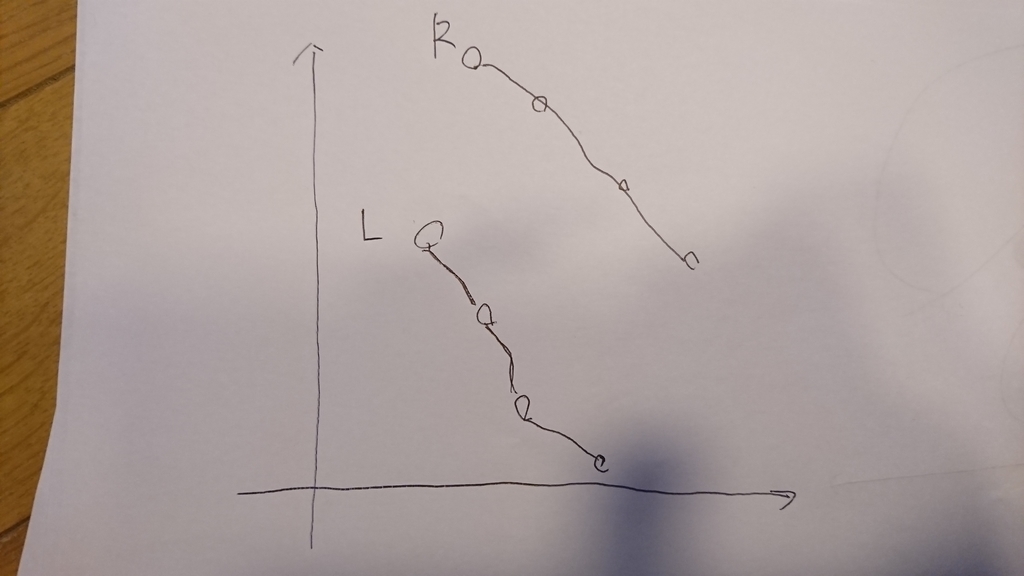
最適な右上が単調増加

もしこの図で

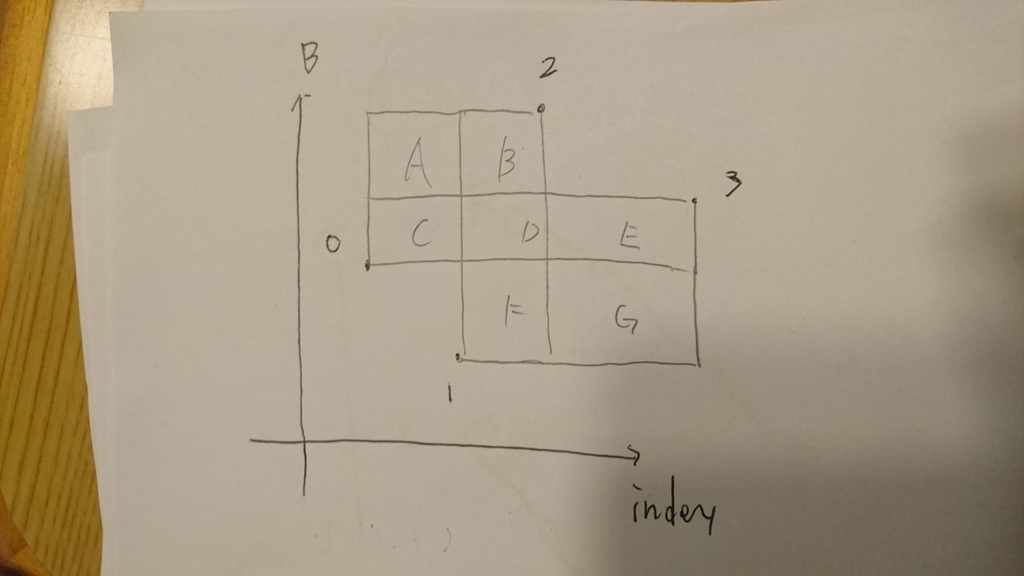
頂点0の最適な右上が3

頂点1の最適な右上が2だとすると

f(0,2) < f(0,3) ==> ABCD < CDE ==> AB < E
f(1,3) < f(1,2) ==> DEFG < BDF ==> EG < B

足すと
ABEG < BE ==> AG < 0(は？)

これは矛盾

つまり

ある左下の頂点Lを決めたときの最適な右上をRとすると、Lより左側の頂点を左下としたときの最適な右上はRより左側、右側についても同様が成り立つ

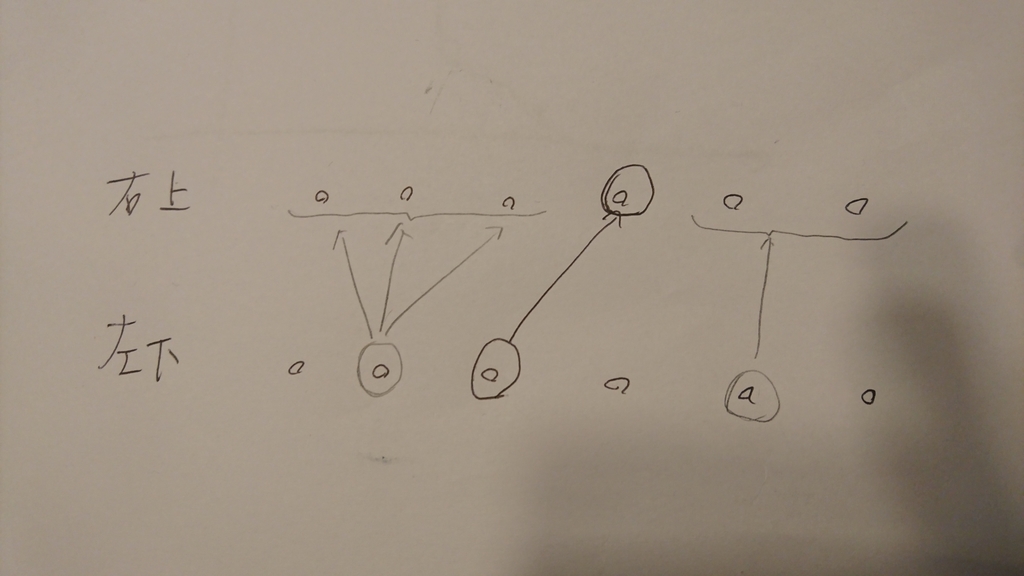
これを使うと,左下の頂点の区間を[left,right),右上の頂点の区間を'[lo,hi)'とすると

(下のsolve関数を見たほうがいいかもしれない)

1.mid = (left + right) / 2番目の左下の頂点をLとする.

2.Lの最適な右上を調べ、indexをrとする.

3.答えを更新

4.[left,mid),[lo,r + 1)に分割して1.をする.

5.[mid + 1,right),[r,hi)に分割して1.をする.

これで答えがO(NlogN)で求まります(すごい)

Source

#include <bits/stdc++.h>
using namespace std;
using i64 = long long;
#define rep(i,s,e) for(int (i) = (s);(i) <= (e);(i)++)
#define all(x) x.begin(),x.end()

class MaxSquare{
public:
  using P = pair<i64,i64>;
  vector<P> L,R;

  vector<P> normalize(vector<P> v){
    vector<P> ret;
    for(int i = 0;i < v.size();i++){
      while(ret.size() > 0 && ret[ret.size() - 1].second <= v[i].second){
        ret.pop_back();
      }
      ret.push_back(v[i]);
    }
    return ret;
  }

  vector<P> flip(vector<P> v){
    for(int i = 0;i < v.size();i++){
      v[i].second *= -1;
    }
    reverse(v.begin(),v.end());
    return v;
  }

  i64 solve(int left,int right,int lo,int hi){
    int mid = (left + right) / 2;
    int bestl = -1;
    i64 best = -1;
    for(int i = lo;i < hi;i++){
      i64 cur = (L[mid].first - R[i].first) * (L[mid].second - R[i].second);
      if(cur > best){
        best = cur;
        bestl = i;
      }
    }

    if(left < mid){
      best = max(best,solve(left,mid,lo,bestl + 1));
    }
    if(mid + 1 < right){
      best = max(best,solve(mid + 1,right,bestl,hi));
    }
    return best;
  }

  i64 getMaxSum(i64 n,i64 s,i64 q,i64 o,vector<i64> x,vector<i64> y){

    vector<i64> b(n);
    rep(i,0,n - 1){
      b[i] = (s / (1LL << 20)) % q + o;

      i64 s0 = (s * 621) % (1LL << 51);
      i64 s1 = (s * 825) % (1LL << 51);
      i64 s2 = (s * 494) % (1LL << 51);
      i64 s3 = (s *  23) % (1LL << 51);

      s = s3;
      s = (s * (1LL << 10) + s2) % (1LL << 51);
      s = (s * (1LL << 10) + s1) % (1LL << 51);
      s = (s * (1LL << 10) + s0 + 11) % (1LL << 51);
    }
    for(int i = 0;i < x.size();i++){
      b[x[i]] = y[i];
    }
    auto X = b;
    for(int i = 1;i < n;i++){
      b[i] += b[i - 1];
    }
    vector<P> B;
    B.push_back({-1,0});
    for(int i = 0;i < n;i++){
      B.push_back({i,b[i]});
    }
    L = flip(normalize(flip(B)));
    R = normalize(B);

    i64 ans = 2 * solve(0,L.size(),0,R.size());
    if(ans == 0){
      ans = 2 * X[0];
      for(int i = 0;i < n;i++){
        ans = max(ans , 2 * X[i]);
      }
    }
    return ans;
  }
};