グラフ抽象化と次元拡張ダイクストラのポエム
ポエムです
完全に趣味です... お見苦しいかも知れません....
それでも, 僕は頑張りました...(4回グラフ抽象化ライブラリの書き直しをしました)(しんどい)
認めてくれたらありがたい限りです. (承認欲求をやめなさーい)
抽象化?
SegmentTreeの抽象化が一番有名なんじゃないかと思っています.
抽象化すると様々なパターンに対応できるほか, 理論として確実に学ぶことができるというメリットがあります(要出典).
SegmentTree, LazySegmentTreeは抽象化してるよという人
class Dinic {
}
とか
class PrimalDual {
}
とかのライブラリを持っている人多いんじゃないかなと思います. それは美しいですか??
速さを求めに来た人, ここでお別れです.
僕なりの抽象化の目的
抽象化すると
みたいなメリットがあります.
抽象化の例
ここではダイクストラ法を出してみます.
Rustにて, https://github.com/kutimoti/mochi-graph-algorithms より
use graph::kernel::graph::*; use graph::kernel::property::*; use graph::kernel::Properties; use std::collections::BinaryHeap; use std::cmp::Ordering; // DijkstraNode ... C++のstd::pairの代わり struct DijkstraNode<W: NNegWeight, V: Vertex> { dist: W, ver : V, } impl<W: NNegWeight, V: Vertex> Ord for DijkstraNode<W, V> { fn cmp(&self, other: &Self) -> Ordering { other.dist.cmp(&self.dist) } } impl<W: NNegWeight, V: Vertex> PartialOrd for DijkstraNode<W, V> { fn partial_cmp(&self, other: &Self) -> Option<Ordering> { Some(other.dist.cmp(&self.dist)) } } impl<W: NNegWeight, V: Vertex> PartialEq for DijkstraNode<W, V> { fn eq(&self, other: &Self) -> bool { self.dist == other.dist } } // ここからDijkstra pub fn dijkstra<'a, G, W, F>(g: &'a G, s: &G::VType, cost: F) -> Properties<W> where G: Graph<'a>, W: NNegWeight, F: Fn(&G::AEType) -> W { let n = g.v_size(); let mut dist = Properties::new(n, &W::inf()); dist[s] = W::zero(); let mut heap = BinaryHeap::new(); heap.push(DijkstraNode { dist: dist[s], ver: s.clone() }); while let Some(DijkstraNode { dist: d, ver: ref v}) = heap.pop() { if dist[v] < d { continue } for ref e in g.delta(v) { if dist[e.from()] + cost(e) < dist[e.to()] { dist[e.to()] = dist[e.from()] + cost(e); heap.push(DijkstraNode{ dist: dist[e.to()], ver: e.to().clone() }) } } } dist }
一つ一つ見ていきます.
引数
pub fn dijkstra<'a, G, W, F>(g: &'a G, s: &G::VType, cost: F) -> Properties<W>
where G: Graph<'a>, W: NNegWeight, F: Fn(&G::AEType) -> W {
dijkstraは, 3つ引数を受け取っていますが, その前に where 以降の部分を解決しましょう.
G: Graph<'a> は G がグラフの構造を持つ型であることを表します.
W: NNegWeight は W が非負の重みであることを表しています.
F: Fn(&G::AEType) -> W は F が &G::AEType を引数とし, W を返す関数であることを表します.
&G::AEType は G の 隣接リストの辺の参照を表す型です.
引数を見ていきます.
g... グラフのデータs... グラフの始点 (G::VType ...Gの頂点の型)cost.. グラフの各辺に対応するcost関数 (E -> Wの写像)
一般的な(???)実装では, costは
struct edge {
int to;
int cost;
}
みたいにしていますが, 関数化することでメリットがあります. (2つ目の目的です)
実装
Dijkstraの動き方を知っている人であれば, Rustを知らなくても全然読めると思います.
Wikipediaの疑似コードと比べても差異がかなり無いと思います.
再利用
例として, 全点間最短パスをポテンシャルを使ってダイクストラを V 回して O(V (E logV)) で求めるアルゴリズムを見てみます.
pub fn dijkstra_with_potential<'a, G, W, F>(g: &'a G, cost: F) -> Option<Properties<Properties<W>>> where G: Directed<'a>, W: ArbWeight + SubtractableWeight, F: Fn(&G::AEType) -> W, <W as ToNNegWeight>::Output: ToArbWeight<Output=W> { let n = g.v_size(); if let Some(pi) = feasible_potential(g, |e| cost(e)) { let mut dist = Properties::new(n, &Properties::new(n, &W::inf())); for s in g.vertices() { let ndist = dijkstra(g, s, |e| (cost(e) + pi[e.from()] - pi[e.to()]).to_nnegw()); for t in g.vertices() { dist[s][t] = ndist[t].to_arbw() + pi[t] - pi[s]; } } Some(dist) } else { None } }
実行可能ポテンシャルが求められた -> g の各頂点 s からダイクストラをする.
というのを完全に表しています. 気持ちいい
次元拡張ダイクストラ
拡張ダイクストラとか言ってませんよね?
yukicoderに出たこれを解こうとすると, 頂点は
#[derive(Clone, PartialEq, Eq, Copy)] //無視して
enum VIP {
Yet,
Used,
}
#[derive(Clone, PartialEq, Eq, Copy)] //無視して
struct Ver(usize, VIP); //(usize, VIP)のタプル
impl ID for Ver { //管理するためのIDを定義
fn id(&self) -> usize {
self.0 + match self.1 {
VIP::Yet => 0,
VIP::Used => 100000,
}
}
}
と, こんな感じになり, 辺は入力 (u, v, d) に対して
g.add_edge((Ver(v, VIP::Yet), Ver(u, VIP::Yet), d)); g.add_edge((Ver(v, VIP::Used), Ver(u, VIP::Used), d)); g.add_edge((Ver(v, VIP::Yet), Ver(u, VIP::Used), 0)); //VIPを使うときは重み0 //無向グラフなので逆辺も g.add_edge((Ver(u, VIP::Yet), Ver(v, VIP::Yet), d)); g.add_edge((Ver(u, VIP::Used), Ver(v, VIP::Used), d)); g.add_edge((Ver(u, VIP::Yet), Ver(v, VIP::Used), 0));
のようになります.
このグラフをダイクストラするだけです. ダイクストラは拡張していません
解法
このコード,
- 重みの抽象化 (非負, 任意の数, ∞, -∞の扱い)
- 頂点, 辺, グラフの抽象化
- 有向グラフの実装
- ダイクストラの実装
- main
を含んでいるのでかなり長いです. ですが, 結果ほとんどのアルゴリズムに対応できる形になりました.
pub trait Zero { fn zero() -> Self; } impl Zero for usize { fn zero() -> Self { 0 } } impl Zero for u64 { fn zero() -> Self { 0 } } impl Zero for u32 { fn zero() -> Self { 0 } } impl Zero for u16 { fn zero() -> Self { 0 } } impl Zero for u8 { fn zero() -> Self { 0 } } impl Zero for isize { fn zero() -> Self { 0 } } impl Zero for i64 { fn zero() -> Self { 0 } } impl Zero for i32 { fn zero() -> Self { 0 } } impl Zero for i16 { fn zero() -> Self { 0 } } impl Zero for i8 { fn zero() -> Self { 0 } } pub trait IsNN {} impl IsNN for usize {} impl IsNN for u64 {} impl IsNN for u32 {} impl IsNN for u16 {} impl IsNN for u8 {} pub trait IsNum: ToNNeg + ToArb { } impl<N: ToNNeg + ToArb> IsNum for N { } pub trait ToNNeg { type Output: Zero + IsNum + IsNN + std::ops::Add<Output=Self::Output> + std::ops::Sub<Output=Self::Output> + std::cmp::Ord + Copy; fn to_nneg(&self) -> Self::Output; } impl ToNNeg for usize { type Output = usize; fn to_nneg(&self) -> Self::Output { self.clone() } } impl ToNNeg for u64 { type Output = u64; fn to_nneg(&self) -> Self::Output { self.clone() } } impl ToNNeg for u32 { type Output = u32; fn to_nneg(&self) -> Self::Output { self.clone() } } impl ToNNeg for u16 { type Output = u16; fn to_nneg(&self) -> Self::Output { self.clone() } } impl ToNNeg for u8 { type Output = u8; fn to_nneg(&self) -> Self::Output { self.clone() } } impl ToNNeg for isize { type Output = usize; fn to_nneg(&self) -> Self::Output { match self.clone() { num if num >= 0 => num as Self::Output, _ => unreachable!() } } } impl ToNNeg for i64 { type Output = u64; fn to_nneg(&self) -> Self::Output { match self.clone() { num if num >= 0 => num as Self::Output, _ => unreachable!() } } } impl ToNNeg for i32 { type Output = u32; fn to_nneg(&self) -> Self::Output { match self.clone() { num if num >= 0 => num as Self::Output, _ => unreachable!() } } } impl ToNNeg for i16 { type Output = u16; fn to_nneg(&self) -> Self::Output { match self.clone() { num if num >= 0 => num as Self::Output, _ => unreachable!() } } } impl ToNNeg for i8 { type Output = u8; fn to_nneg(&self) -> Self::Output { match self.clone() { num if num >= 0 => num as Self::Output, _ => unreachable!() } } } pub trait ToArb { type Output: Zero + IsNum + std::ops::Add<Output=Self::Output> + std::ops::Sub<Output=Self::Output> + std::cmp::Ord + Copy; fn to_arb(&self) -> Self::Output; } impl ToArb for isize { type Output = isize; fn to_arb(&self) -> Self::Output { self.clone() } } impl ToArb for i64 { type Output = i64; fn to_arb(&self) -> Self::Output { self.clone() } } impl ToArb for i32 { type Output = i32; fn to_arb(&self) -> Self::Output { self.clone() } } impl ToArb for i16 { type Output = i16; fn to_arb(&self) -> Self::Output { self.clone() } } impl ToArb for i8 { type Output = i8; fn to_arb(&self) -> Self::Output { self.clone() } } impl ToArb for usize { type Output = isize; fn to_arb(&self) -> Self::Output { self.clone() as isize } } impl ToArb for u64 { type Output = i64; fn to_arb(&self) -> Self::Output { self.clone() as i64 } } impl ToArb for u32 { type Output = i32; fn to_arb(&self) -> Self::Output { self.clone() as i32 } } impl ToArb for u16 { type Output = i16; fn to_arb(&self) -> Self::Output { self.clone() as i16 } } impl ToArb for u8 { type Output = i8; fn to_arb(&self) -> Self::Output { self.clone() as i8 } } pub trait Integer: Sized + std::ops::Shl<usize, Output=Self> + std::ops::Shr<usize, Output=Self> {} impl Integer for usize {} impl Integer for u64 {} impl Integer for u32 {} impl Integer for u16 {} impl Integer for u8 {} impl Integer for isize {} impl Integer for i64 {} impl Integer for i32 {} impl Integer for i16 {} impl Integer for i8 {} /// Trait for properties. pub trait Property: Copy {} impl<P> Property for P where P: Copy {} /// Types implementing `ToNNegWeight` are able to convert to non-negative weights. /// This trait use the algorithms with potentials (`dijkstra_with_potential`, etc...). pub trait ToNNegWeight { /// converting type. type Output: NNegWeight; /// convert to non-negative weights. fn to_nnegw(&self) -> Self::Output; } /// Types implementing `ToARbWeight` are able to convert to arbitrary weights. /// This trait use to reverse from non-negative weight after converting weight. pub trait ToArbWeight { /// converting type. type Output: ArbWeight; /// convert to non-negative weights. fn to_arbw(&self) -> Self::Output; } /// Trait of arbitrary weights. /// the arbirary weight has infinity, zero and negative infinity. pub trait ArbWeight where Self: ToNNegWeight + ToArbWeight + Property + std::ops::Add<Output=Self> + std::cmp::Ord { fn inf() -> Self; fn zero() -> Self; fn neg_inf() -> Self { unreachable!() } } /// Trait of non-negative weights. pub trait NNegWeight where Self: ArbWeight {} /// Trait of weights of integer. /// types implementing this use the scaling algorithms. pub trait IntegerWeight: ArbWeight + std::ops::Shl<usize, Output=Self> + std::ops::Shr<usize, Output=Self> {} impl<W> IntegerWeight for W where W: ArbWeight + std::ops::Shl<usize, Output=Self> + std::ops::Shr<usize, Output=Self> {} pub trait SubtractableWeight: ArbWeight + std::ops::Sub<Output=Self> {} impl<W> SubtractableWeight for W where W: ArbWeight + std::ops::Sub<Output=Self> {} /// Trait of capacity for maxflow, mcf, and so on. pub trait Capacity: ArbWeight + IntegerWeight + SubtractableWeight {} impl<W> Capacity for W where W: ArbWeight + IntegerWeight + SubtractableWeight {} pub trait Cost<Cap>: ArbWeight + SubtractableWeight + std::ops::Mul<Cap, Output=Self> {} impl<Co, Cap> Cost<Cap> for Co where Cap: Capacity, Co: ArbWeight + SubtractableWeight + SubtractableWeight + std::ops::Mul<Cap, Output=Self> {} /// Trait for elements of graph (Vertex, Edge, ...) that have ID (usize). /// the elements implementing ID are able to use [`graph::kernel::Properties`]. pub trait ID { /// return id of the element. fn id(&self) -> usize; } /// Implementing ID for usize. impl ID for usize { /// return the own value fn id(&self) -> usize { *self } } /// Trait for vertices of graphs. pub trait Vertex: ID + Eq + Copy { } impl<V: ID + Eq + Copy> Vertex for V { } /// Trait for edges of graphs. pub trait Edge { /// Vertex type at both ends of edge type VType: Vertex; /// Start point of edge fn from(&self) -> &Self::VType; /// End point of edge fn to(&self) -> &Self::VType; } /// Implementing Edge for the simple tuple. impl<V> Edge for (V, V) where V: Vertex { type VType = V; fn from(&self) -> &Self::VType { &self.0 } fn to(&self) -> &Self::VType { &self.1 } } /// Implementing Edge for the simple tuple. impl<V, P> Edge for (V, V, P) where V: Vertex, P: Property { type VType = V; fn from(&self) -> &Self::VType { &self.0 } fn to(&self) -> &Self::VType { &self.1 } } /// Trait for adjacency edges of graph. /// Why do we use [`Edge`] as is? There are 2 reasons. /// - To give values to the edges to use Properties (AdjEdge has ID). /// - When using a undirected graph as a directed graph, must swap two ends of edge. pub trait AdjEdge: ID + Edge { /// Edge type of raw edge. type EType: Edge<VType=Self::VType>; /// return raw edge. fn edge(&self) -> &Self::EType; } /// Trait for adjcency edges on ResidualNetwork. /// It has reverse edge. pub trait ResidualEdge: AdjEdge { fn rev(&self) -> Self; } /// Trait of graph. pub trait Graph<'a> { /// Type of vertices. type VType: Vertex + 'a; /// Type of edges. type EType: Edge<VType=Self::VType>; /// Type of adjacency edges. type AEType: AdjEdge<VType=Self::VType, EType=Self::EType>; /// Type of iterator for adjacency list. type AdjIter: std::iter::Iterator<Item=Self::AEType>; /// Type of iterator for edges list. type EIter: std::iter::Iterator<Item=Self::AEType>; /// Type of iterator for vertices list. type VIter: std::iter::Iterator<Item=&'a Self::VType>; /// return adjacency list from the vertex v. fn delta(&'a self, v: &Self::VType) -> Self::AdjIter; /// return edges list. fn edges(&'a self) -> Self::EIter; /// return vertices list. fn vertices(&'a self) -> Self::VIter; /// return the number of vertices. fn v_size(&self) -> usize; /// return the number of edges. fn e_size(&self) -> usize; } /// Trait of directed graph. pub trait Directed<'a>: Graph<'a> {} /// Trait of undirected graph. /// graphs implementing this hold that the edge `(v, u)` exists for the edge `(u, v)` when the graph /// use as directed graph pub trait Undirected<'a>: Graph<'a> {} /// Trait of bipartite graph. pub trait Bipartite<'a>: Undirected<'a> { /// Type of iterator for vertices in one side. type BVIter: std::iter::Iterator<Item=&'a Self::VType>; /// return vertices list in left side. fn left_vertices(&'a self) -> Self::BVIter; /// return vertices list in right side. fn right_vertices(&'a self) -> Self::BVIter; } /// Trait of residual network /// `AEType` must be `ResidualEdge`. pub trait Residual<'a>: Directed<'a> where <Self as Graph<'a>>::AEType: ResidualEdge {} pub fn generate_func<AE, P, F>(f: F) -> impl Fn(&AE) -> P where AE: AdjEdge, P: Property, F: Fn(&AE::EType) -> P { move |ae| f(ae.edge()) } use std::ops::{ Index, IndexMut }; #[derive(Clone)] pub struct Properties<W: Clone> { vec: Vec<W> } impl<'a, I: ID, W: Clone> Index<&'a I> for Properties<W> { type Output = W; fn index(&self, idx: &'a I) -> & Self::Output { &self.vec[idx.id()] } } impl<'a, I: ID, W: Clone> IndexMut<&'a I> for Properties<W> { fn index_mut(&mut self, idx: &'a I) -> &mut Self::Output { &mut self.vec[idx.id()] } } impl<'a, W: Clone> Properties<W> { pub fn new(n: usize, init: &W) -> Self { Properties { vec: vec![init.clone(); n], } } pub fn iter(&'a self) -> std::slice::Iter<'a, W> { self.vec.iter() } } #[derive(Clone, Copy, PartialEq, Eq)] pub enum ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy { Inf, Some(W), NegInf, } impl<W> std::ops::Add for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn add(self, rhs: Self) -> Self { match self { ArbW::Inf => { match rhs { ArbW::NegInf => unreachable!(), _ => ArbW::Inf, } } ArbW::Some(d) => { match rhs { ArbW::Inf => ArbW::Inf, ArbW::Some(d2) => ArbW::Some(d + d2), ArbW::NegInf => ArbW::NegInf, } } ArbW::NegInf => { match rhs { ArbW::Inf => unreachable!(), _ => ArbW::NegInf, } } } } } impl<W> std::ops::Sub for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::ops::Sub<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn sub(self, rhs: Self) -> Self { match self { ArbW::Inf => { match rhs { ArbW::Inf => unreachable!(), _ => ArbW::Inf, } } ArbW::Some(d) => { match rhs { ArbW::Inf => ArbW::NegInf, ArbW::Some(d2) => ArbW::Some(d - d2), ArbW::NegInf => ArbW::Inf, } } ArbW::NegInf => { match rhs { ArbW::NegInf => unreachable!(), _ => ArbW::NegInf, } } } } } impl<W,X> std::ops::Mul<ArbW<X>> for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy + std::ops::Mul<Output=W>, X: Zero + IsNum + std::ops::Add<Output=X> + std::cmp::Ord + Copy + Into<W> { type Output = Self; fn mul(self, rhs: ArbW<X>) -> Self { match self { ArbW::Inf => { match rhs { ArbW::NegInf => ArbW::NegInf, _ => ArbW::Inf, } } ArbW::Some(d) => { match rhs { ArbW::Inf => ArbW::Inf, ArbW::Some(d2) => ArbW::Some(d.mul(d2.into())), ArbW::NegInf => ArbW::NegInf, } } ArbW::NegInf => { match rhs { ArbW::NegInf => ArbW::Inf, _ => ArbW::NegInf, } } } } } impl<W,X> std::ops::Mul<NNegW<X>> for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy + std::ops::Mul<Output=W>, X: Zero + IsNum + IsNN + std::ops::Add<Output=X> + std::cmp::Ord + Copy + Into<W> { type Output = Self; fn mul(self, rhs: NNegW<X>) -> Self { match self { ArbW::Inf => { ArbW::Inf } ArbW::Some(d) => { match rhs { NNegW::Inf => ArbW::Inf, NNegW::Some(d2) => ArbW::Some(d.mul(d2.into())), } } ArbW::NegInf => { ArbW::NegInf } } } } impl<W> std::cmp::PartialOrd for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy { fn partial_cmp(&self, rhs: &Self) -> Option<std::cmp::Ordering> { Some(self.cmp(rhs)) } } impl<W> std::cmp::Ord for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy { fn cmp(&self, rhs: &Self) -> std::cmp::Ordering { match self { ArbW::Inf => { match rhs { ArbW::Inf => std::cmp::Ordering::Equal, _ => std::cmp::Ordering::Greater, } } ArbW::Some(d) => { match rhs { ArbW::Inf => std::cmp::Ordering::Less, ArbW::Some(d2) => d.cmp(d2), ArbW::NegInf => std::cmp::Ordering::Greater, } } ArbW::NegInf => { match rhs { ArbW::NegInf => std::cmp::Ordering::Equal, _ => std::cmp::Ordering::Less, } } } } } impl<W> ToNNegWeight for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = NNegW<<W as ToNNeg>::Output>; fn to_nnegw(&self) -> Self::Output { match self { ArbW::Inf => NNegW::Inf, ArbW::Some(ref num) => NNegW::Some(num.to_nneg()), ArbW::NegInf => unreachable!(), } } } impl<W> ToArbWeight for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn to_arbw(&self) -> Self::Output { self.clone() } } impl<W> std::ops::Shl<usize> for ArbW<W> where W: Zero + IsNum + Integer + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn shl(self, rhs: usize) -> Self { match self { ArbW::Some(d) => ArbW::Some(d.shl(rhs)), inf => inf, } } } impl<W> std::ops::Shr<usize> for ArbW<W> where W: Zero + IsNum + Integer + std::ops::Add<Output=W> + std::cmp::Ord + Copy + std::ops::Shr<usize, Output=W> { type Output = Self; fn shr(self, rhs: usize) -> Self { match self { ArbW::Some(d) => ArbW::Some(d.shr(rhs)), inf => inf, } } } impl<W> ArbWeight for ArbW<W> where W: Zero + IsNum + std::ops::Add<Output=W> + std::cmp::Ord + Copy { fn inf() -> Self { ArbW::Inf } fn zero() -> Self { ArbW::Some(W::zero()) } fn neg_inf() -> Self { ArbW::NegInf } } #[derive(Clone, Copy, PartialEq, Eq)] pub enum NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy { Inf, Some(W), } impl<W> std::ops::Add for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn add(self, rhs: Self) -> Self { match self { NNegW::Inf => { NNegW::Inf } NNegW::Some(d) => { match rhs { NNegW::Inf => NNegW::Inf, NNegW::Some(d2) => NNegW::Some(d + d2), } } } } } impl<W> std::ops::Sub for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::ops::Sub<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn sub(self, rhs: Self) -> Self { match self { NNegW::Inf => { match rhs { NNegW::Inf => unreachable!(), _ => NNegW::Inf, } } NNegW::Some(d) => { match rhs { NNegW::Inf => unreachable!(), NNegW::Some(d2) => NNegW::Some(d - d2), } } } } } impl<W> std::cmp::PartialOrd for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy { fn partial_cmp(&self, rhs: &Self) -> Option<std::cmp::Ordering> { Some(self.cmp(rhs)) } } impl<W> std::cmp::Ord for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy { fn cmp(&self, rhs: &Self) -> std::cmp::Ordering { match self { NNegW::Inf => { match rhs { NNegW::Inf => std::cmp::Ordering::Equal, _ => std::cmp::Ordering::Greater, } } NNegW::Some(d) => { match rhs { NNegW::Inf => std::cmp::Ordering::Less, NNegW::Some(d2) => d.cmp(d2), } } } } } impl<W> IsNN for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy {} impl<W> ToNNegWeight for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn to_nnegw(&self) -> Self::Output { self.clone() } } impl<W> ToArbWeight for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = ArbW<<W as ToArb>::Output>; fn to_arbw(&self) -> Self::Output { match self { NNegW::Inf => ArbW::Inf, NNegW::Some(ref num) => ArbW::Some(num.to_arb()) } } } impl<W> std::ops::Shl<usize> for NNegW<W> where W: Zero + IsNum + IsNN + Integer + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn shl(self, rhs: usize) -> Self { match self { NNegW::Some(d) => NNegW::Some(d.shl(rhs)), other => other, } } } impl<W> std::ops::Shr<usize> for NNegW<W> where W: Zero + IsNum + IsNN + Integer + std::ops::Add<Output=W> + std::cmp::Ord + Copy { type Output = Self; fn shr(self, rhs: usize) -> Self { match self { NNegW::Some(d) => NNegW::Some(d.shr(rhs)), other => other, } } } impl<W> ArbWeight for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy { fn inf() -> Self { NNegW::Inf } fn zero() -> Self { NNegW::Some(W::zero()) } } impl<W> NNegWeight for NNegW<W> where W: Zero + IsNum + IsNN + std::ops::Add<Output=W> + std::cmp::Ord + Copy {} #[derive(Clone,Copy,Eq,PartialEq,Debug)] pub struct Eite(pub usize); pub struct DiAdjEdge<'a, E: Edge + 'a>(&'a E, usize); impl<'a, E: Edge + 'a> ID for DiAdjEdge<'a, E> { fn id(&self) -> usize { self.1 } } impl<'a, E> Edge for DiAdjEdge<'a, E> where E: Edge + 'a { type VType = E::VType; fn from(&self) -> &E::VType { self.0.from() } fn to(&self) -> &E::VType { self.0.to() } } impl<'a, E> AdjEdge for DiAdjEdge<'a, E> where E: Edge + 'a { type EType = E; fn edge(&self) -> &E { self.0 } } pub struct AdjIter<'a, E: Edge + 'a> { iter: std::slice::Iter<'a, Eite>, edges: &'a Vec<E>, } impl<'a, E: Edge + 'a> std::iter::Iterator for AdjIter<'a, E> { type Item = DiAdjEdge<'a, E>; fn next(&mut self) -> Option<Self::Item> { match self.iter.next() { Some(ei) => { Some( DiAdjEdge(&self.edges[ei.0], ei.0) ) } None => { None } } } } pub struct EIter<'a, E: Edge + 'a> { i: usize, iter: std::slice::Iter<'a, E>, } impl<'a, E: Edge + 'a> std::iter::Iterator for EIter<'a, E> { type Item = DiAdjEdge<'a, E>; fn next(&mut self) -> Option<Self::Item> { match self.iter.next() { Some(e) => { let i = self.i; self.i += 1; Some(DiAdjEdge(&e, i)) } None => None } } } pub struct VIter<'a, V: Vertex + 'a> { iter: std::slice:: Iter<'a, Option<V>>, } impl<'a, V: Vertex + 'a> std::iter::Iterator for VIter<'a, V> { type Item = &'a V; fn next(&mut self) -> Option<Self::Item> { while let Some(v) = self.iter.next() { if v.is_none() { continue; } else { return v.as_ref() } } None } } pub struct DirectedGraph<V: Vertex, E: Edge<VType=V>> { n: usize, m: usize, g: Vec<Vec<Eite>>, es: Vec<E>, vs: Vec<Option<V>>, } impl<'a, V, E> Graph<'a> for DirectedGraph<V,E> where V: Vertex + 'a, E: Edge<VType=V> + 'a { type VType = V; type EType = E; type AEType = DiAdjEdge<'a, E>; type AdjIter = AdjIter<'a, E>; type EIter = EIter<'a, E>; type VIter = VIter<'a, V>; fn delta(&'a self, v: &V) -> Self::AdjIter { AdjIter { iter: self.g[v.id()].iter(), edges: &self.es } } fn edges(&'a self) -> Self::EIter { EIter { i: 0, iter: self.es.iter() } } fn vertices(&'a self) -> Self::VIter { VIter { iter: self.vs.iter() } } fn v_size(&self) -> usize { self.n } fn e_size(&self) -> usize { self.m } } impl<V: Vertex, E: Edge<VType=V>> DirectedGraph<V,E> { pub fn new(n: usize) -> Self { DirectedGraph { n: n, m: 0, g: vec![Vec::<Eite>::new(); n], es: Vec::new(), vs: vec![None; n], } } fn vertex_regist(&mut self, v: V) { let i = v.id(); self.vs[i] = match self.vs[v.id()].take() { Some(vv) => { assert!(vv.id() == v.id()); Some(vv) } None => { Some(v) } } } pub fn add_edge(&mut self, e: E) { let ei = Eite(self.m); self.m += 1; self.g[e.from().id()].push(ei); self.vertex_regist(e.from().clone()); self.vertex_regist(e.to().clone()); self.es.push(e); } } impl<'a, V, E> Directed<'a> for DirectedGraph<V, E> where V: Vertex + 'a, E: Edge<VType=V> + 'a {} use std::collections::BinaryHeap; use std::cmp::Ordering; struct DijkstraNode<W: NNegWeight, V: Vertex> { dist: W, ver : V, } impl<W: NNegWeight, V: Vertex> Ord for DijkstraNode<W, V> { fn cmp(&self, other: &Self) -> Ordering { other.dist.cmp(&self.dist) } } impl<W: NNegWeight, V: Vertex> PartialOrd for DijkstraNode<W, V> { fn partial_cmp(&self, other: &Self) -> Option<Ordering> { Some(other.dist.cmp(&self.dist)) } } impl<W: NNegWeight, V: Vertex> PartialEq for DijkstraNode<W, V> { fn eq(&self, other: &Self) -> bool { self.dist == other.dist } } impl<W: NNegWeight, V: Vertex> Eq for DijkstraNode<W, V> { } pub fn dijkstra<'a, G, W, F>(g: &'a G, s: &G::VType, cost: F) -> Properties<W> where G: Graph<'a>, W: NNegWeight, F: Fn(&G::AEType) -> W { let n = g.v_size(); let mut dist = Properties::new(n, &W::inf()); dist[s] = W::zero(); let mut heap = BinaryHeap::new(); heap.push(DijkstraNode { dist: dist[s], ver: s.clone() }); while let Some(DijkstraNode { dist: d, ver: ref v}) = heap.pop() { if dist[v] < d { continue } for ref e in g.delta(v) { if dist[e.from()] + cost(e) < dist[e.to()] { dist[e.to()] = dist[e.from()] + cost(e); heap.push(DijkstraNode{ dist: dist[e.to()], ver: e.to().clone() }) } } } dist } #[derive(Clone, PartialEq, Eq, Copy)] enum VIP { Yet, Used, } #[derive(Clone, PartialEq, Eq, Copy)] struct Ver(usize, VIP); impl ID for Ver { fn id(&self) -> usize { self.0 + match self.1 { VIP::Yet => 0, VIP::Used => 100000, } } } fn main() { /* input start */ let mut s = String::new(); std::io::stdin().read_line(&mut s).unwrap(); let v:Vec<usize> = s.trim().split_whitespace() .map(|e|e.parse().unwrap()).collect(); let (n, m) = (v[0] , v[1]); /* input end */ let mut g = DirectedGraph::new(200000); for _ in 0..m{ /* input start */ let mut t = String::new(); std::io::stdin().read_line(&mut t).unwrap(); let x:Vec<usize> = t.trim().split_whitespace() .map(|e|e.parse().unwrap()).collect(); let (v, u, d) = (x[0] - 1, x[1] - 1, x[2]); /* input end */ g.add_edge((Ver(v, VIP::Yet), Ver(u, VIP::Yet), d)); g.add_edge((Ver(v, VIP::Used), Ver(u, VIP::Used), d)); g.add_edge((Ver(v, VIP::Yet), Ver(u, VIP::Used), 0)); g.add_edge((Ver(u, VIP::Yet), Ver(v, VIP::Yet), d)); g.add_edge((Ver(u, VIP::Used), Ver(v, VIP::Used), d)); g.add_edge((Ver(u, VIP::Yet), Ver(v, VIP::Used), 0)); } g.add_edge((Ver(0, VIP::Yet), Ver(0, VIP::Used), 0)); let res = dijkstra(&g, &Ver(0, VIP::Yet), |ep| NNegW::Some(ep.edge().2)); for i in 0..n { let ans = res[&Ver(i, VIP::Yet)] + res[&Ver(i, VIP::Used)]; if let NNegW::Some(d) = ans { println!("{}", d); } } }
抽象化して嬉しいこと
以下はマジであったことです.
Edmonds-Karp's Capacity Scaling Minimum Cost B-Flow というアルゴリズムの実装をしていて,
そのアルゴリズムの中で Dijkstraを使うのですが, Dijkstraで扱う重みは非負である必要があります.
C++で一度実装していてAOJで通っていたので, イケるやろと思って上の抽象化に合わせて書き直したらassertが出たんですね...
その値はNonNegativeではありません ってね
バグを抽象化の機構で見つけることが出来たんですね. 最高です(そのアルゴはまだ作れていないので最悪です)
言いたかったこと
これを見せたかっただけです. (本当にごめんなさい)
くちもちとくらの重み付き最大マッチング実装日記 - priority queue 2の実装
http://kutimoti.hatenablog.com/entry/2018/11/14/194510
前回です
今回でわかったんですけど,日記なので前回の実装ミスったとか普通にあります
p.q.2 とは
p.q.2(priority queue 2)も重み付き最大マッチングで高速化に使われるものです.p.q.1を使って実装します.
p.q.2ではp.q.1とは違ってグループに要素が優先度付きで挿入されていきます.
それぞれのグループにはactiveかnonactiveの設定がされていて
p.q.2ではactiveなグループに含まれている要素の中で一番優先度の低いものを答えるクエリを捌きます
操作は以下です.
- [insert]要素
iを優先度p_iでグループgに挿入する. - [erase]要素
iを削除する. - [find]activeなグループに含まれている要素の中で優先度の一番小さい要素を見つける.
- [subtract_delta]activeなグループに挿入されているすべての要素の優先度をδだけ小さくする.
- [generate new group]新しいグループを作る
- [delete group]グループを削除する.
- [change active status]グループのactive状態を変更する.
- [split]要素iを含んでいるグループをi以下の要素のグループとiより大きいグループで分ける.
p.q.2 の実装方針
まず,グループを追加していくのは面倒臭いので,必要なグループの数をコンストラクタで指定させることにしました.
(5),(6)の削除の操作も処理が多くなるので,(5),(6)を併合してclear()としました.
pqA[g]はグループgに属する要素を管理するp.q.1です._isActive[g]はグループgがactiveかどうかをboolで持ったものです.pqBはそれぞれのactiveなグループからfindした値を入れたものです(つまりこれをfindすれば,p.q.2のfindが達成できます)delta_last[g]は操作1,2,7,8を行ったときのpqB::delta(論文中ではΔと表現されている)の値です.これを保持することで,操作4によるグループ間の値の変化をうまく処理することが出来ます.(処理しているのはeval_delta)group[i]は要素iが属しているグループです.erase_from_BでpqBからグループgの最小の優先度の要素を取り除き,insert_to_BでpqBにグループgの最小の優先度の要素を挿入します.これにより,active状態を変更したときの挙動や,グループにinsert,eraseしたときのpqBに対する処理が出来ます.
注意
この実装のために,前回のsplay_mqとpq_1を変更しました.
splay_mq
mq_index()の返す型をKeyからPに変えました(p.q.2で最小の優先度を取得する必要があったため)
pq_1
それに伴ってfind()の返す型を::std::pair<priority_type,element_type>に変えました.
実装
pq_2
#include <vector> class pq_2{ using element_type = int; using priority_type = long long; using group_type = ::std::size_t; priority_type delta; const ::std::size_t N; const ::std::size_t G; ::std::vector<pq_1*> pqA; ::std::vector<bool> _isActive; ::std::vector<priority_type> delta_last; ::std::vector<group_type> group; pq_1 pqB; void eval_delta(group_type g){ if(_isActive[g]){ pqA[g]->delta = pqA[g]->delta + pqB.delta - delta_last[g]; } delta_last[g] = pqB.delta; } void erase_from_B(group_type g){ if(_isActive[g]){ auto p = pqA[g]->find(); if(p.second == -1) return; pqB.erase(p.second); } } void insert_to_B(group_type g){ if(_isActive[g]){ auto p = pqA[g]->find(); if(p.second == -1) return; pqB.insert(p.second , p.first - pqA[g]->delta); } } public: pq_2(::std::size_t ele_num , ::std::size_t group_num) : N(ele_num) , G(group_num){ pqA.assign(G , nullptr); _isActive.assign(G , false); delta_last.assign(G , 0); group.assign(N , -1); for(int i = 0;i < G;i++){ pqA[i] = new pq_1(); } } ~pq_2(){ for(auto & pqa : pqA){ if(pqa) delete pqa , pqa = nullptr; } } // (1) insert an element i with priority pi to group g void insert(group_type g , element_type i , priority_type pi){ eval_delta(g); erase_from_B(g); pqA[g]->insert(i,pi); group[i] = g; insert_to_B(g); } // (2) delete an element i void erase(element_type i){ pqA[group[i]]->erase(i); group_type g = group[i]; erase_from_B(g); pqB.erase(i); group[i] = -1; insert_to_B(g); } // (3) find an active element with the minimal priority ::std::pair<priority_type,element_type> find(){ return pqB.find(); } // (4) decrease the priorityies of all the active elements by some real numbers delta void subtract_delta(priority_type d){ pqB.subtract_delta(d); } // (5) and (6) delete a group g and generate a new empty group(nonactive) void clear(group_type g){ erase_from_B(g); delete pqA[g] , pqA[g] = nullptr; pqA[g] = new pq_1(); _isActive[g] = false; delta_last[g] = pqB.delta; } // (7.1) change the status of a group from nonactive to active void activate(group_type g){ eval_delta(g); _isActive[g] = true; insert_to_B(g); } // (7.2) change the status of a group from active to nonactive void nonactivate(group_type g){ eval_delta(g); erase_from_B(g); _isActive[g] = false; } // (8) split a group according to an element in it void split(element_type i , group_type save_to){ group_type g = group[i]; if(g == -1) return; eval_delta(g); auto p = pqA[g]->tree->split(i); delete pqA[g]->tree; pqA[g]->tree = p.first; pqA[save_to]->tree = p.second; } };
次回
何もわかっていないので僕が論文を読んでからのお楽しみ
くちもちとくらの重み付き最大マッチング実装日記 - priority queue 1の実装
これからこの論文にもとづいて
重み付き最大マッチングをO(EVlogV)で実装するアルゴリズムを書いていきたいと思います.よろしくお願いします.
またkutimoti/MaximalWeightedMatching - GitHubでソースコードは見られます.
言語はC++です.
p.q.1 とは
p.q.1(priority queue 1)はこの重み付き最大マッチングで高速化をするために必要なデータ構造です.またp.q.2でも使います.
操作は以下の4つです.
- [insert]要素
iを優先度p_iで挿入する. - [erase]要素を削除する.
- [mq_index]優先度の一番小さい要素を見つける.
- [subtract_delta]挿入されているすべての優先度をδだけ小さくする.
p.q.1 の実装方針
splay tree(平衡二分木) でAOJ RMQのように実装します.
insert , eraseの操作は平衡二分木なのでできます.
splay tree の各頂点に部分木の中で最小の優先度p_iと要素iを持つstd::pair<int,int> mq = {p_i , i}をもってやることで,findにも答えられます.
subtract_deltaは,Δ = Σδを持っておくことで,次からのinsertをp_i + Δで挿入することで,挿入されている優先度を引き算せずに,優先度を並べることを達成できます.
実装
splay tree
splay tree の実装はSplay tree - Wikipediaが一番わかりやすいです.
#include <algorithm> #include <set> class splay_mq{ using i64 = long long; using Key = i64; using T = i64; using P = ::std::pair<T,Key>; const long long INF = 1e18; const P PINF = {INF , -1}; struct node{ node* left; node* right; node* parent; Key key; T value; P mq; node(const Key& key , const T& val) : left(nullptr) , right(nullptr) , parent(nullptr) , key(key) , value(val) , mq({val , key}){} ~node(){ if(left) delete left , left = nullptr; if(right) delete right , right = nullptr; } }; node* root; T get_value(const node* n){ if(!n) return INF; return n->value; } P get_mq(const node* n){ if(!n) return PINF; return n->mq; } node* fix(node * n){ if(!n) return nullptr; n->mq = ::std::min(::std::min(get_mq(n->left) , get_mq(n->right)) , {get_value(n) , n->key}); return n; } void set_left(node * par , node * x){ if(par) par->left = x; if(x) x->parent = par; fix(par); } void set_right(node * par , node * x){ if(par) par->right = x; if(x) x->parent = par; fix(par); } void zig(node * x){ node* p = x->parent; set_left(p,x->right); if(p->parent){ if(p->parent->left == p) set_left(p->parent , x); else set_right(p->parent , x); } else{ x->parent = nullptr; } set_right(x , p); } void zag(node * x){ node* p = x->parent; set_right(p,x->left); if(p->parent){ if(p->parent->left == p) set_left(p->parent , x); else set_right(p->parent , x); } else{ x->parent = nullptr; } set_left(x , p); } node* splay(node* x){ if(!x) return nullptr; while(x->parent){ if(!x->parent->parent){ if(x->parent->left == x){ zig(x); } else{ zag(x); } } else if(x->parent->parent->left == x->parent && x->parent->left == x){ zig(x->parent); zig(x); } else if(x->parent->parent->left == x->parent && x->parent->right == x){ zag(x->parent); zig(x); } else if(x->parent->parent->right == x->parent && x->parent->right == x){ zag(x->parent); zag(x); } else{ zig(x->parent); zag(x); } } return root = x; } public: splay_mq() : root(nullptr){} splay_mq(node * root) : root(root){} ~splay_mq(){if(root) delete root , root = nullptr; } bool find(const Key& key){ node * z = root; node* p = nullptr; while(z){ p = z; if(z->key < key) z = z->right; else if(key < z->key) z = z->left; else{ splay(z); return true; } } splay(p); return false; } void insert(Key key , T val){ if(find(key)) return; node* z = new node(key,val); if(!root) root = z; else if(root->key < key){ set_right(z , root->right); set_right(root , z); } else{ set_left(z , root->left); set_left(root , z); } splay(z); } bool erase(Key key){ if(!find(key)){ return false; } node * z = root; if(!z->left && !z->right) root = nullptr; else if(!z->left){ root = z->right; root->parent = nullptr; } else if(!z->right){ root = z->left; root->parent = nullptr; } else{ node * lm = z->left; while(lm->right){ lm = lm->right; } z->left->parent = nullptr; splay(lm); root = lm; set_right(root , z->right); } fix(root); return true; } Key mq_index(){ return get_mq(root).second; } ::std::pair<splay_mq*,splay_mq*> split(Key key){ if(!root) return {new splay_mq() , new splay_mq()}; find(key); splay_mq* ngr ,* gr; if(root->key <= key){ root->right->parent = nullptr; gr = new splay_mq(root->right); root->right = nullptr; fix(root); ngr = new splay_mq(root); } else{ root->left->parent = nullptr; ngr = new splay_mq(root->left); root->left = nullptr; fix(root); gr = new splay_mq(root); } root = nullptr; return {ngr , gr}; } };
pq_1
class pq_1{ public: using element_type = long long; using priority_type = long long; priority_type delta; splay_mq *tree; pq_1() : delta(0) , tree(new splay_mq()){} pq_1(splay_mq * tr) : delta(0) , tree(tr){} ~pq_1(){if(tree) delete tree , tree = nullptr;} // (1) insert an element i with priority pi void insert(element_type i , priority_type pi){ tree->insert(i , pi + delta); } // (2) delete an element i void erase(element_type i){ tree->erase(i); } // (3) find an element with the minimal priority element_type find(){ return tree->mq_index(); } // (4) subtract from the priorities of all the current elements some real number delta void subtract_delta(priority_type d){ delta += d; } };
次回
p.q.2を実装していきます.
今日から始めるWingBIT - 非再帰SegmentTreeのようなもの
非再帰SegmentTreeと一緒にはしたくない()
経緯
トイレでなんとなく思いついたデータ構造がうまくいったので好きになっているだけの話です(論文があったというのは内緒で)
BIT(BinaryIndexedTree)を知っていますか?
このような感じでそれぞれの要素を持ち,[0,k]の和を求めるデータ構造です.

O(logN)で区間和が取得できる上,SegmentTreeより定数倍が早い,実装が軽いことで有名ですね.
しかし,,,
BITは和以外では使いみちがあまりわからない
RMQ(Range Minimum Query)などは処理することができません...悲しいね
そこで†WingBIT†なるものを紹介します.
WingBIT

このように今まで空いていたスペースにBITをもう一枚入れる感じのデータ構造です.(名前の由来はここから来ています)
いまから具体的にクエリをどのように捌くか説明します.
点更新 - update
index = 3の場所を更新する例です.
だんだん高さをあげていき,updateをします.
まず,3の真上にあるBlueとRedの場所をマークします.

Blue(3)は一番下のノードなので,値を更新して,次のBlueにマークを移動させます.
移動は+depthをするとできます.

次にdepth=2をみるとRed(6)があります.
これを下の2つのノードを使って更新します.
そして次のRedにマークを移動させます.

depth=4をみるとBlue(4)があります
同じように下の2つのノードを使って更新します.
そして次のBlueにマークを移動させます.
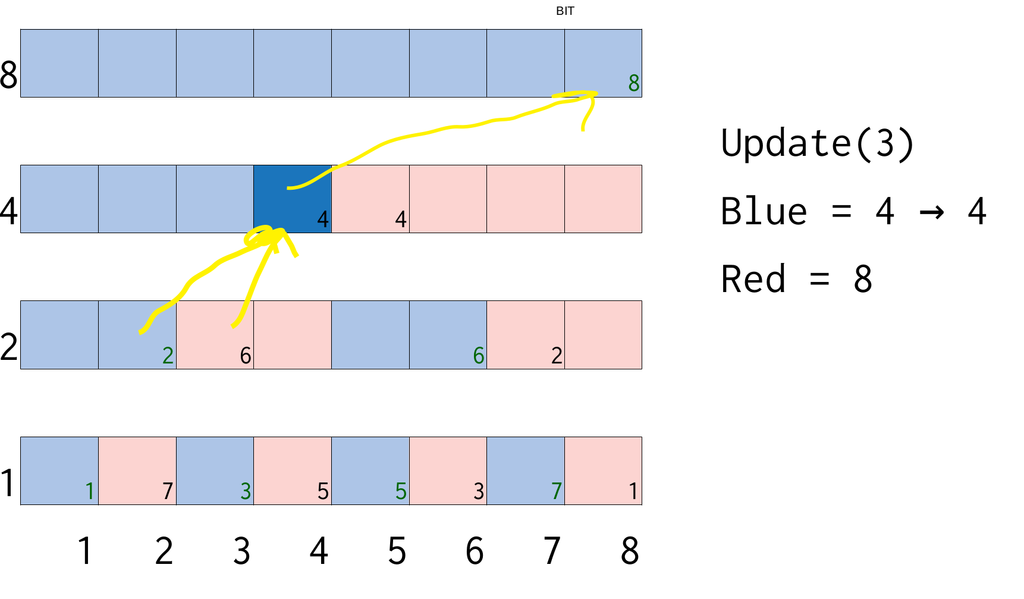
これを繰り返し,depthが一番上に行くまで繰り返すことで,更新が出来ます.
区間取得 - get_inter
一例を見てみましょう.

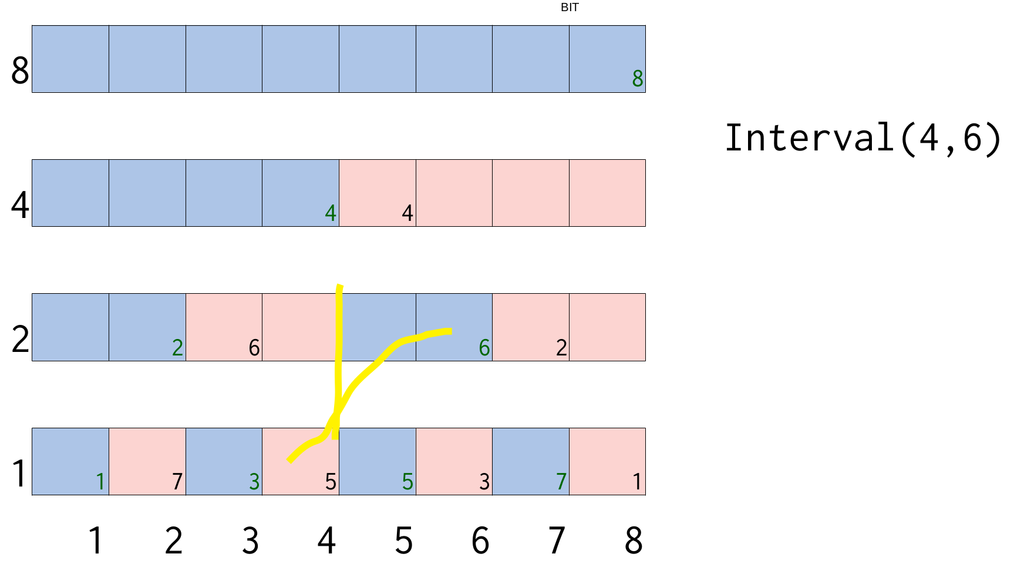
区間は必ず,左側がRed,右側がBlueでできていませんか?これを使って実装していきます.(RedとBlueでWingが出来ています.)
先と同じように下から処理していきます.
左側をRedにマーク,右側をBlueにマークします.

depth=1を見ると,Blue(7)があります.これは区間の一部なので,利用していきます.
次の位置は-depthをすることで移動できます.

depth=2を見ると,Red(6),Blue(6)があります.これも区間の一部なので,利用します.

RedとBlueが交差したので終了です.
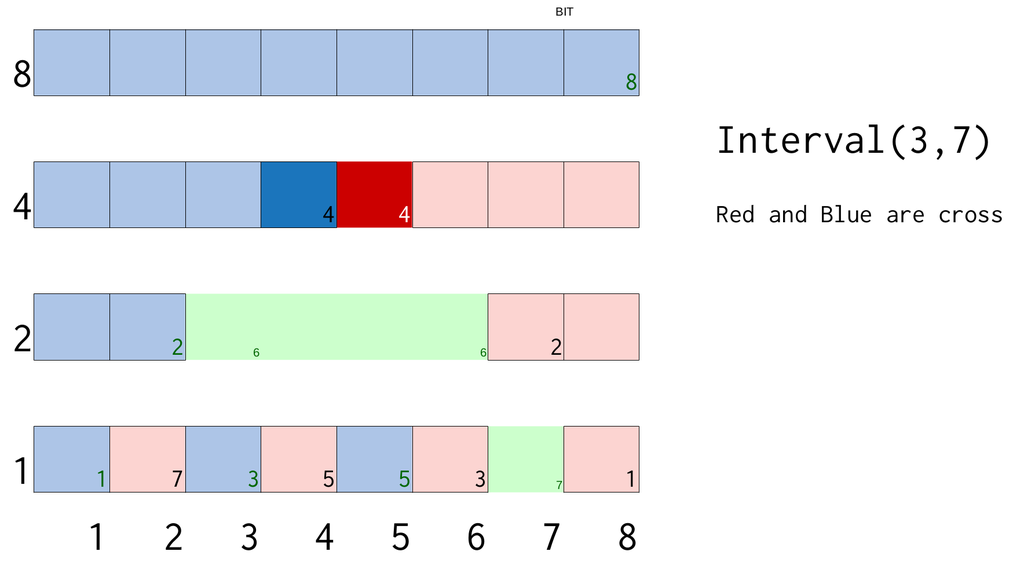
実装例
Nim Langで書いています.
shl...左シフト shr...右シフト seq...C++のvectorと思っていただければ
import algorithm type WingBIT[Monoid] = object rw : seq[Monoid] lw : seq[Monoid] ide : Monoid sz : int update_func : proc(node : Monoid , x : Monoid) : Monoid f : proc(x : Monoid , y : Monoid) : Monoid proc newWingBIT*[Monoid](n : int , ide : Monoid, update_func : proc(node : Monoid , x : Monoid) : Monoid , f : proc(x : Monoid , y : Monoid) : Monoid) : WingBIT[Monoid] = var bit : WingBIT[Monoid] bit.rw = @[] bit.lw = @[] bit.sz = 1 while bit.sz < n: bit.sz = bit.sz * 2 bit.rw.setLen(bit.sz + 1) bit.lw.setLen(bit.sz + 1) bit.rw.fill(ide) bit.lw.fill(ide) bit.ide = ide bit.update_func = update_func bit.f = f return bit proc update*[Monoid](bit : var WingBIT[Monoid] , k : int , x : Monoid) = var depth = 1 var right = k var left = bit.sz + 1 - k if (right and depth) > 0: bit.rw[right] = bit.update_func(bit.rw[right],x) right = right + depth if (left and depth) > 0: bit.lw[left] = bit.update_func(bit.lw[left],x) left = left + depth depth = 2 while depth <= bit.sz: var dd = depth shr 1 if (left and depth) > 0: bit.lw[left] = bit.f(bit.rw[bit.sz - left + dd],bit.lw[left - dd]) left = left + depth if (right and depth) > 0: bit.rw[right] = bit.f(bit.rw[right - dd],bit.lw[bit.sz - right + dd]) right = right + depth depth = depth shl 1 proc get_inter*[Monoid](bit : WingBIT[Monoid] , left : int , right : int) : Monoid = var al = bit.ide var ar = bit.ide var depth = 1 var l = bit.sz + 1 - left var r = right while bit.sz + 1 - l <= r: if (l != bit.sz) and ((l and depth) > 0): al = bit.f(al,bit.lw[l]) l -= depth if (r and depth) > 0: ar = bit.f(bit.rw[r],ar) r -= depth depth = depth shl 1 return bit.f(ar,al) # verify arc008 - d import strutils import sequtils var temp = stdin.readLine.split.map(parseInt) var N = temp[0] var M = temp[1] var p : array[101010,int64] var a : array[101010,float64] var b : array[101010,float64] var se : seq[int64] = @[] for i in 0..<M: var temp2 = stdin.readLine.split p[i] = temp2[0].parseInt a[i] = temp2[1].parseFloat b[i] = temp2[2].parseFloat se.add(p[i]) sort(se,system.cmp) type TT = tuple[a : float64 , b : float64] proc ffunc(x : TT,y : TT) : TT= return (y.a * x.a , y.a * x.b + y.b) proc uupdate(x : TT,y : TT) : TT= return y var ran = newWingBIT(M + 1000,(1.0,0.0),uupdate,ffunc) var mr : float64 = 1.0 var ir : float64 = 1.0 for i in 0..<M: p[i] = lowerBound(se,p[i]) + 1 ran.update((int)p[i],(a[i],b[i])) var tup : TT = ran.rw[ran.sz] var rrr : float64 = tup.a + tup.b mr = max(mr,rrr) ir = min(ir,rrr) echo ir.formatFloat echo mr.formatFloat
利点
再帰SegmentTreeより早い.(無駄が無い)
実装がそんなに大変なわけでもない
名前がかっこいい
SRM 735 MaxSquare 「よくある二分探索の変なことをやるやつ」
なんやこのテク...っていう気持ちになったので記事を書きます
http://community.topcoder.com/stat?c=problem_statement&pm=14929
問題の解説...https://www.topcoder.com/blog/single-round-match-735-editorials/
りんごさんの参考解説動画(ICPCの類似した問題)
https://youtu.be/agCN6bPxeE4?t=6052
https://youtu.be/agCN6bPxeE4?t=11979
問題の本質
数列Bが与えられる. このときf(i,j) = (B[j] - B[i]) * (j - i + 1)の最大値を求めよ.
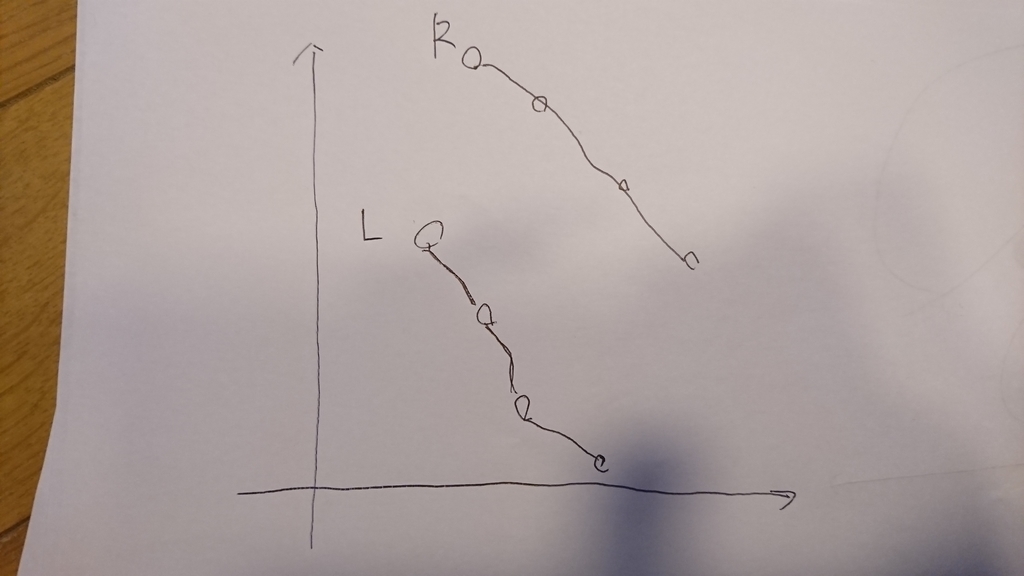
平面で考えてみる
横軸をindex,縦軸をBの値のと置くと、下のような図ができて
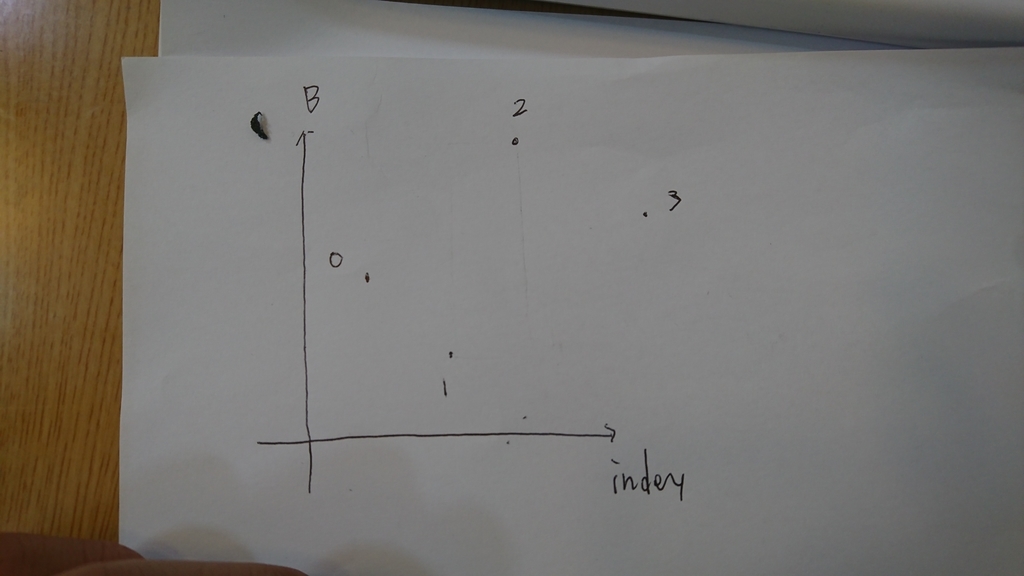
この図でf(1,2)は、下の長方形の面積になります.'

これの最大を求めたい...
最適な右上
ある頂点iを決めたとき、f(i,j)が最大になるjを「最適な右上」と呼ぶことにします.
左下になり得る頂点、右上になり得る頂点
こんな感じになりそう(実際なって証明ができるがなんとなくわかる)
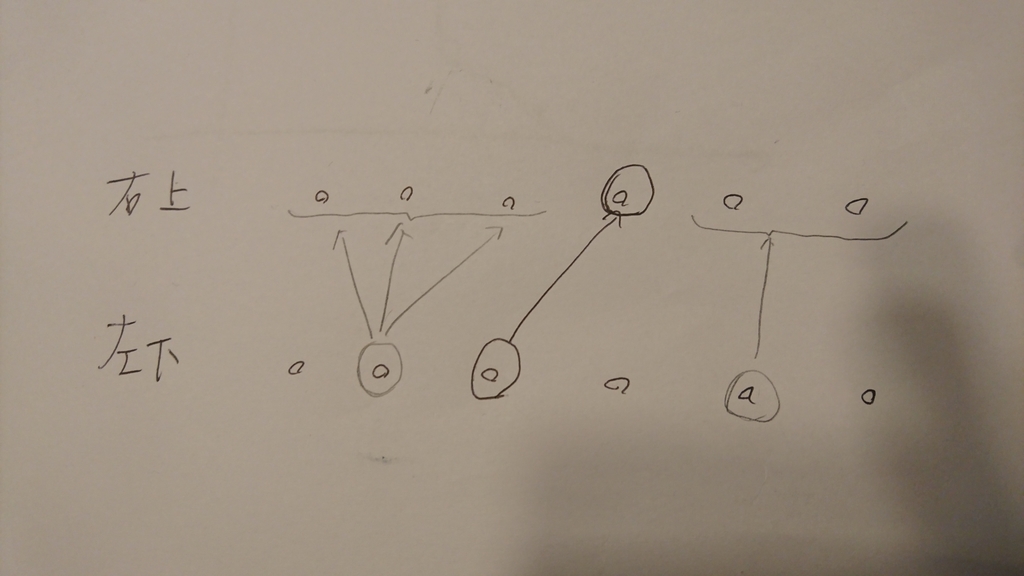
最適な右上が単調増加
もしこの図で
頂点0の最適な右上が3
頂点1の最適な右上が2だとすると
f(0,2) < f(0,3) ==> ABCD < CDE ==> AB < E f(1,3) < f(1,2) ==> DEFG < BDF ==> EG < B 足すと ABEG < BE ==> AG < 0(は?)
これは矛盾
つまり
ある左下の頂点Lを決めたときの最適な右上をRとすると、Lより左側の頂点を左下としたときの最適な右上はRより左側、右側についても同様が成り立つ
これを使うと,左下の頂点の区間を[left,right),右上の頂点の区間を'[lo,hi)'とすると
(下のsolve関数を見たほうがいいかもしれない)
1.mid = (left + right) / 2番目の左下の頂点をLとする.
2.Lの最適な右上を調べ、indexをrとする.
3.答えを更新
4.[left,mid),[lo,r + 1)に分割して1.をする.
5.[mid + 1,right),[r,hi)に分割して1.をする.
これで答えがO(NlogN)で求まります(すごい)
Source
#include <bits/stdc++.h> using namespace std; using i64 = long long; #define rep(i,s,e) for(int (i) = (s);(i) <= (e);(i)++) #define all(x) x.begin(),x.end() class MaxSquare{ public: using P = pair<i64,i64>; vector<P> L,R; vector<P> normalize(vector<P> v){ vector<P> ret; for(int i = 0;i < v.size();i++){ while(ret.size() > 0 && ret[ret.size() - 1].second <= v[i].second){ ret.pop_back(); } ret.push_back(v[i]); } return ret; } vector<P> flip(vector<P> v){ for(int i = 0;i < v.size();i++){ v[i].second *= -1; } reverse(v.begin(),v.end()); return v; } i64 solve(int left,int right,int lo,int hi){ int mid = (left + right) / 2; int bestl = -1; i64 best = -1; for(int i = lo;i < hi;i++){ i64 cur = (L[mid].first - R[i].first) * (L[mid].second - R[i].second); if(cur > best){ best = cur; bestl = i; } } if(left < mid){ best = max(best,solve(left,mid,lo,bestl + 1)); } if(mid + 1 < right){ best = max(best,solve(mid + 1,right,bestl,hi)); } return best; } i64 getMaxSum(i64 n,i64 s,i64 q,i64 o,vector<i64> x,vector<i64> y){ vector<i64> b(n); rep(i,0,n - 1){ b[i] = (s / (1LL << 20)) % q + o; i64 s0 = (s * 621) % (1LL << 51); i64 s1 = (s * 825) % (1LL << 51); i64 s2 = (s * 494) % (1LL << 51); i64 s3 = (s * 23) % (1LL << 51); s = s3; s = (s * (1LL << 10) + s2) % (1LL << 51); s = (s * (1LL << 10) + s1) % (1LL << 51); s = (s * (1LL << 10) + s0 + 11) % (1LL << 51); } for(int i = 0;i < x.size();i++){ b[x[i]] = y[i]; } auto X = b; for(int i = 1;i < n;i++){ b[i] += b[i - 1]; } vector<P> B; B.push_back({-1,0}); for(int i = 0;i < n;i++){ B.push_back({i,b[i]}); } L = flip(normalize(flip(B))); R = normalize(B); i64 ans = 2 * solve(0,L.size(),0,R.size()); if(ans == 0){ ans = 2 * X[0]; for(int i = 0;i < n;i++){ ans = max(ans , 2 * X[i]); } } return ans; } };
AtCoder Regular Contest 074 E - RGB Sequence
https://beta.atcoder.jp/contests/arc074/tasks/arc074_c
解法
左から色を決めていくとする.
すでに塗った部分の色をすべて覚えておくことはできないので、情報量を落とさなければならない.
どうしよう?
ここで問題の性質である色の種類がxiであるについて考える.
区間に色を含んでいることはどうやってわかるだろう...?
これは,各色の一番右の場所を覚えておけば良い.
なので,i番目のマスを更新する際.i == rとなる与えられている区間[l,r]について,
遷移元の状態がx種類であるかどうかを見てやれば良い.
なので
dp[i + 1][i + 1][g][b] += dp[i][r][g][b]; //g,bについても同様に
である.
しかし、これでは間に合わない.
よく見ると,i = max({r,g,b})であるので,遷移を縮めることができる.
これでOK.
#include <bits/stdc++.h> using namespace std; using i64 = long long; #define rep(i,s,e) for(int (i) = (s);(i) <= (e);(i)++) int N,M; vector<int> L,R,X; vector<int> ri[303]; i64 dp[303][303][303]; i64 MOD = 1e9 + 7; int main(){ cin >> N >> M; L.resize(M); R.resize(M); X.resize(M); rep(i,0,M - 1) cin >> L[i] >> R[i] >> X[i]; rep(i,0,M - 1) ri[R[i]].push_back(i); dp[0][0][0] = 1; rep(r,0,N - 1){ rep(g,0,N - 1){ rep(b,0,N - 1){ int next = max({r,g,b}) + 1; //red { bool ok = true; int MIN = min({g,b}); int MAX = max({g,b}); for(auto idx : ri[next]){ int cnt = 1; if(MAX >= L[idx]) cnt++; if(MIN >= L[idx]) cnt++; ok = ok && cnt == X[idx]; } if(ok){ dp[next][g][b] += dp[r][g][b]; dp[next][g][b] %= MOD; } } { bool ok = true; int MIN = min({r,b}); int MAX = max({r,b}); for(auto idx : ri[next]){ int cnt = 1; if(MAX >= L[idx]) cnt++; if(MIN >= L[idx]) cnt++; ok = ok && cnt == X[idx]; } if(ok){ dp[r][next][b] += dp[r][g][b]; dp[r][next][b] %= MOD; } } { bool ok = true; int MIN = min({g,r}); int MAX = max({g,r}); for(auto idx : ri[next]){ int cnt = 1; if(MAX >= L[idx]) cnt++; if(MIN >= L[idx]) cnt++; ok = ok && cnt == X[idx]; } if(ok){ dp[r][g][next] += dp[r][g][b]; dp[r][g][next] %= MOD; } } } } } i64 ans = 0; rep(i,0,N - 1){ rep(j,0,N - 1){ ans = (dp[N][i][j] + ans) % MOD; ans = (dp[i][N][j] + ans) % MOD; ans = (dp[i][j][N] + ans) % MOD; } } cout << ans << endl; }
AtCoder Regular Contest 100 E - Or Plus Max
問題URL : https://beta.atcoder.jp/contests/arc100/tasks/arc100_c
問題
長さ2^Nの整数列A(0-indexed)がある. 1 <= K <= 2^N - 1を満たすすべての整数 K について, 次の値を求める. 0 <= i < j <= 2^N - 1,(i or j) <= K のとき, A_i + A_jの最大値を求めよ.
問題を見て思ったこと
(i or j) <= K から i < j <= K であることがわかる.
(i or j) <= Kなので,うまくbitDPをしそう...
考察
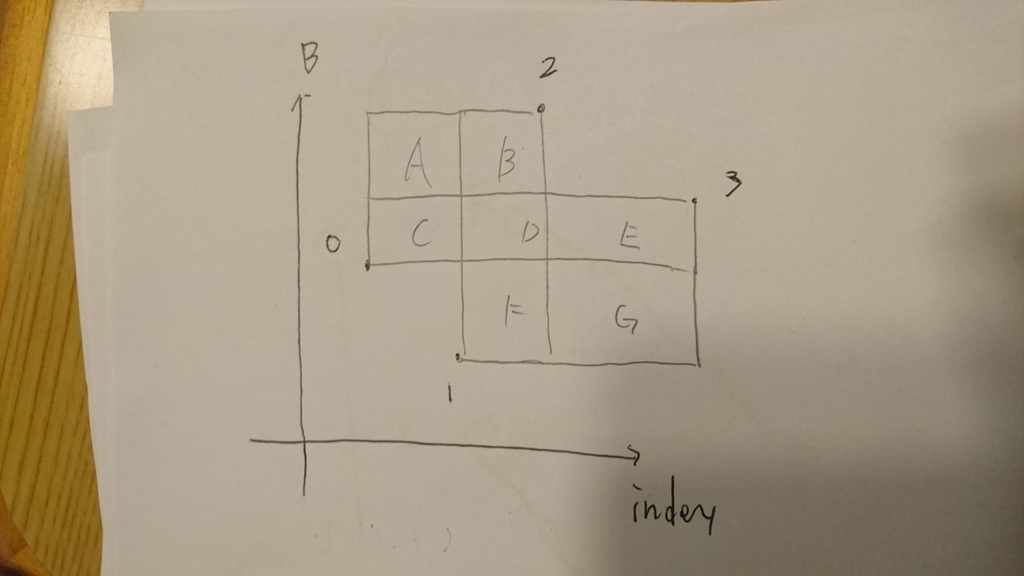
入力例3について考えてみます.
次のように,最大値を2番目まで持つことでうまくやることができます.

i = 0 のときの MAX1st,MAX2nd を作る.

ここで,最大値と同時にiの値も記録するのが大事です(後で説明します)
K = 1のときの値を求める

K = 1のときは j = 0,1 が選べるので,MAX1st[i]の値は75に,MAX2nd[i]の値は26になります.
ここでMAX1st[i] + MAX2nd[i]を取ると,K = 1のときの答えが得られます.
K = 2のときの値を求める.
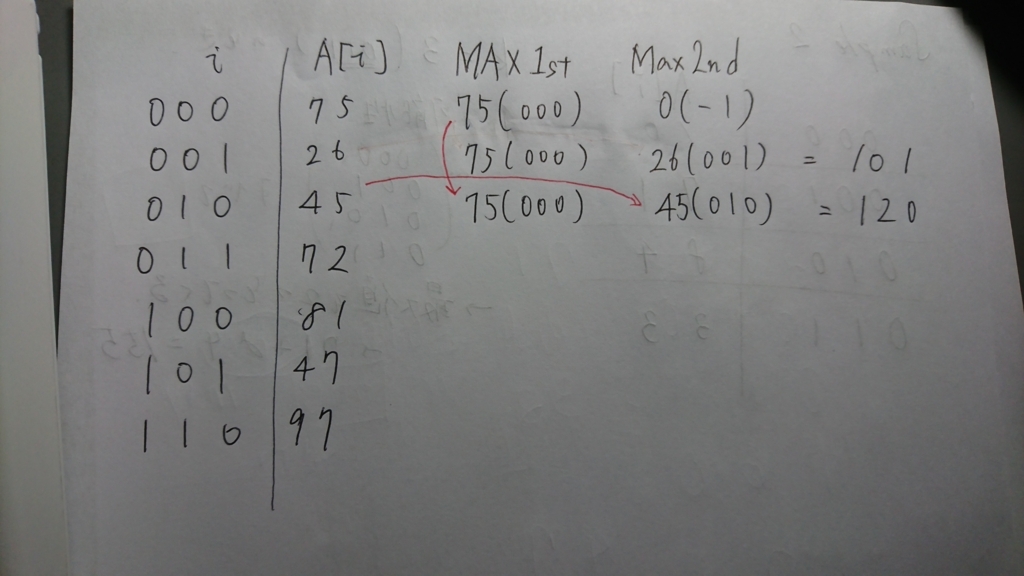
K = 2のときは j = 0,2 が選べるので,MAX1st[i]の値は75に,MAX2nd[i]の値は45になります.
ここでMAX1st[i] + MAX2nd[i]を取ると,K = 1のときの答えが得られます.
K = 3のときの値を求める.

ここが大事です.
K = 3のときは j = 0,1,2が選べますが,
j = 0 を見る必要はあるでしょうか?ないですね.
なぜなら,j = 0 の値は j = 1,2 ですでに評価されています(その結果,MAX1stが75になっている)
なので,見るべきは K = 3からビットを一つづつ消した,j = 1,2だけでOKです.
また,青色の矢印がバツされています.なぜでしょう?
これはi < jの条件です.重複を防いでいます.これのためにMAX2ndを用意しています.
これを繰り返すことで (i or j) == K のときの値を計算できます.
(i or j) <= K
(i or j) == K について考えていたので,後は今までの最大値を取るだけでOKです.
source code
resとans要らない(草)
#include <bits/stdc++.h> using namespace std; using i64 = long long; #define rep(i,s,e) for(int (i) = (s);(i) <= (e);(i)++) #define all(x) x.begin(),x.end() int N; vector<i64> A; vector<i64> ans; vector<i64> MAX[2]; vector<i64> mi[2]; vector<i64> res; int main(){ cin >> N; A.resize(1 << N); ans.resize(1 << N,0); MAX[0].resize(1 << N,0); MAX[1].resize(1 << N,0); mi[0].resize(1 << N,0); mi[1].resize(1 << N,0); res.resize(1 << N,0); rep(i,0,(1 << N) - 1) cin >> A[i]; MAX[0][0] = A[0]; mi[0][0] = 0; ans[0] = A[0]; res[0] = A[0]; int cnt = 0; rep(s,1,(1 << N) - 1){ vector<pair<i64,i64>> vec; vec.push_back({A[s],s}); rep(i,0,N){ if(s & (1 << i)){ vec.push_back({MAX[0][s & ~(1 << i)],mi[0][s & ~(1 << i)]}); vec.push_back({MAX[1][s & ~(1 << i)],mi[1][s & ~(1 << i)]}); } } sort(all(vec)); //重複削除 vec.erase(unique(all(vec)),vec.end()); //最大値なので reverse(all(vec)); if(vec.size() >= 2){ MAX[0][s] = vec[0].first; mi[0][s] = vec[0].second; MAX[1][s] = vec[1].first; mi[1][s] = vec[1].second; ans[s] = MAX[0][s] + MAX[1][s]; } //これ多分要らない else{ MAX[0][s] = vec[0].first; mi[0][s] = vec[0].second; ans[s] = MAX[0][s]; } res[s] = max(ans[s],res[s - 1]); cout << res[s] << endl; } }
うまく説明するのが難しいなぁ...